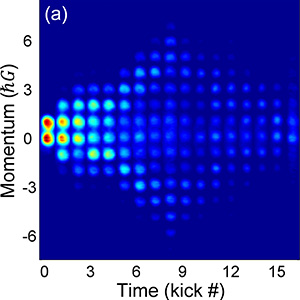
Classical random walks play a key role in modeling stochastic processes and represent a basic component of diffusion phenomena and nondeterministic motion.
They have applications in fields as diverse as astronomy, solid-state physics, polymer chemistry, biology, and computer science. The hope is that quantum versions of random walks can lead to applications unavailable classically. Of particular note is the possibility of using quantum walks in probabilistic algorithms for universal quantum computing. The concept of a classical random walk can be translated into a quantum random walk using the entanglement between different degrees of freedom. In quantum walks, one degree of freedom acts as the "coin" which determines the direction of the walk which occurs in the other degree of freedom. However, a quantum coin can produce a superposition of two (or more states) and therefore the corresponding walk is heavily influenced by the entanglement between the coin and the walk degrees of freedom. In the experiments in Summy’s lab, the "walker" is a Bose-Einstein condensate of rubidium atoms which interacts with a series of microwave and laser pulses to move through momentum space. These experiments represent the first time a quantum walk has been realized in momentum, an important milestone in the creation of multi-dimensional quantum walks. This work is also important for the development of quantum search algorithms which can be much faster than their classical counterparts.
APS Synopsis: Quantum Walk in a Bose-Einstein Condensate
"Quantum Walk in Momentum Space with a Bose-Einstein Condensate," Siamak Dadras, Alexander Gresch, Caspar Groiseau, Sandro Wimberger, and Gil S. Summy. Phys. Rev. Lett. 121, 070402.